The animations were generated with MATLAB software.
Directions: Click on the images to begin the animation.
Continuous Release into a Uniform Flow
Steady 2-D and 3-D solutions
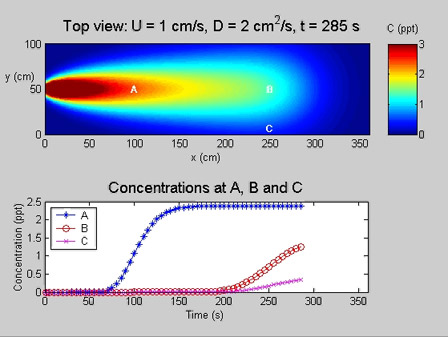
This animation depicts the evolution of the concentration field downstream of a continuous point source in a channel with steady flow (U = 1 cm/s). The concentration is measured at three points. At each point the center of the front, defined by C = 0.5*Cfinal, arrives at the advection time scale, x/U. The duration of the front, which is the time required for the concentration to rise from C=0 to Cfinal, is 4 σ/U, where σ is the length-scale of the front at t = x/U, i.e. σ= sqrt(2Dx/U).
* Note to Unix users: the animation opens up behind active windows.