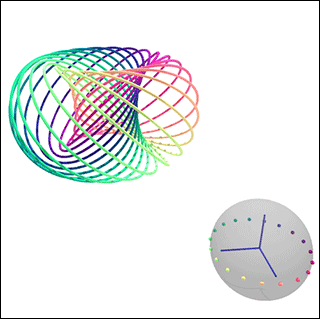
The Hopf fibration shows how the three-sphere can be built by a collection of circles arranged like points on a two-sphere. This is a frame from an animation of fibers in the Hopf fibration over various points on the two-sphere. (Image and animation courtesy of Niles Johnson.
Instructor(s)
Prof. Haynes Miller
MIT Course Number
18.905
As Taught In
Fall 2016
Level
Graduate
Course Description
Course Features
Course Description
This is a course on the singular homology of topological spaces. Topics include: Singular homology, CW complexes, Homological algebra, Cohomology, and Poincare duality.


