Isomorphic Graphs
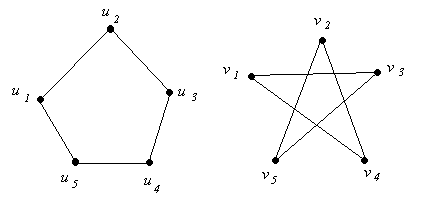
The two graphs above are isomorphic, which means that there exists an edge-preserving bijection from the set of vertices of the graph on the left to the set of vertices of the graph on the right.
How many such bijections are there?
Home » Courses » Electrical Engineering and Computer Science » Mathematics for Computer Science » Unit 2: Structures » 2.8 Degrees & Isomorphism » 2.8.6 Isomorphic Graphs

The two graphs above are isomorphic, which means that there exists an edge-preserving bijection from the set of vertices of the graph on the left to the set of vertices of the graph on the right.
How many such bijections are there?