
Session Overview
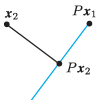 | If the product Ax points in the same direction as the vector x, we say that x is an eigenvector of A. Eigenvalues and eigenvectors describe what happens when a matrix is multiplied by a vector. In this session we learn how to find the eigenvalues and eigenvectors of a matrix. |
Session Activities
Lecture Video and Summary
- Watch the video lecture
Eigenvalues and Eigenvectors (00:51:23)
Lecture 21: Eigenvalues and Eigenvectors
> Download from iTunes U (MP4 - 115MB)
> Download from Internet Archive (MP4 - 115MB)
- Read the accompanying lecture summary (PDF)
- Lecture video transcript (PDF)
Suggested Reading
- Read Section 6.1 through 6.2 in the 4th or 5th edition.
Problem Solving Video
- Watch the recitation video on
Eigenvalues and Eigenvectors (00:09:21)
Problem Solving: Eigenvalues and Eigenvectors
> Download from iTunes U (MP4 - 21MB)
> Download from Internet Archive (MP4 - 21MB)
- Recitation video transcript (PDF)
Check Yourself
Problems and Solutions
Work the problems on your own and check your answers when you're done.
Further Study
Eigenvalue Demonstrations*
These demonstrations employ Java® applets with voice-over narration by Professor Strang.
Mini-lectures on Eigenvalues
These mini-lectures with voice-over narration below help to explain some key Eigenvalue concepts.
- det(A-λI)=0
- Eigenvectors and Trace
- Powers
- Diagonalization
- Differential Equations
- Symmetry
- Positive Definite
- SVD
*Funding for these demonstrations was provided by a grant from the The d'Arbeloff Fund for Excellence in MIT Education as part of The d'Arbeloff Interactive Mathematics Project (d'A I M P).
