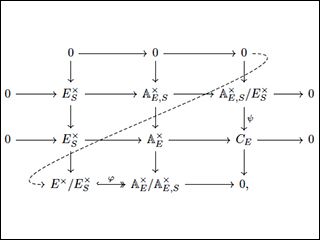
Commutative diagram: the map φ is surjective by the choice of S and is also injective by the definition of ESx. (Courtesy of Oron Propp. Used with permission.)
Instructor(s)
Dr. Sam Raskin
MIT Course Number
18.786
As Taught In
Spring 2016
Level
Graduate
Course Description
Course Features
Course Description
This course is the continuation of 18.785 Number Theory I. It begins with an analysis of the quadratic case of Class Field Theory via Hilbert symbols, in order to give a more hands-on introduction to the ideas of Class Field Theory. More advanced topics in number theory are discussed in this course, such as Galois cohomology, proofs of class field theory, modular forms and automorphic forms, Galois representations, and quadratic forms.


