Flash and JavaScript are required for this feature.
Download the video from iTunes U or the Internet Archive.
Description: This video lecture demonstrates the concept of scope by example of a recursive function that produces the Fibonacci sequence.
Instructor: Yossi Farjoun

Lecture 5: Scripts and Func...
PROFESSOR: This is Dr. [? MATLAB, ?] lecture 5, scripts and functions. The previous lecture we saw the function FtoC that converts Fahrenheit to Celsius. Let's take another look at that function.
Here it is. It's a very simple function. I've changed it around a little bit, but it accepts Fer as input. Cel is output. And this is how we write it.
I could have, of course, written this as a script. And it would have been a much worse idea. Let's try it as a script. I'll comment this out. And I'll comment this out.
And now if I save it, I can change directory to Scripts. I can say Fer equals 80 and now call my FtoC. And now if I look at Cel, it equals the answer.
The problem with this-- there are several problems with this. One is that I need to understand the inner working, my inner notation of the script in order to use it. I need to know that Fer is an input. I need to know that Cel is the output.
So I need to know that before I call the script, I have to assign 80 into Fer. After I call the script, I get the answer inside Cel. I need to know all of that. And of course, most functions are going to be much more complicated than this one-liner.
Another problem is that, obviously since it requires me to write into Fer and write into Cel, it will overwrite Fer and Cel. And particularly, it will overwrite Cel. So if I have an important number in Cel and now I call FtoC, this important number is overwritten. There's nothing I can do about it. Except for changing this script, there's no way I can make it not overwrite Cel.
Now most functions have all kinds of intermediary variables. So ind1 and there's some assignment that goes into it there, and another one, and so on, which are needed for the calculation. These are of course fake ones, but imagine that you had these and now you would call these. Sorry, you would call FtoC again.
You would be littered by these variables that you don't know where they came from. You don't care about them because they're some partial result inside the script. And also they might have overwritten one of your variables. So this could be really a disaster.
This is where scoping is important. When you put this inside a function, even if you keep all the littering the same, now you call this function-- let's clear my variables first. Let's look who's here. No one's here.
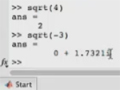
And now I'm going to call FtoC with 80. Again the answer, and the only variable that exists, is this automatic variable called ans. Ans is an automatic variable that is generated when a value is returned, but it's not assigned. So for example, if I do 1 plus 2, there is also an ans. And ans equals 3.
This is useful if, for example-- notice that here I forgot to actually assign this into a variable. So I can now save it by saying, x equals ans. And now my answer is saved into x.
Again, using functions does not litter my work space with partial results. You see ind1, ind2 are contained inside this function, and we do not see them outside. And they make it unnecessary to know the inner workings of the function.
I don't need to know what the inner name of the input variable is and what the inner name of the output variable is. I just need to know that FtoC accepts an input variable and returns a value. I don't need to know the name of those variables.
Scope also allows us to write what's called recursive functions. A classic example of recursive function is the function that creates the Fibonacci sequence. So let's try this. We already had one Fibonacci so let's do Fibbo2.
And it accepts an n. The base case, of course. We need to return a value. And if it's not less than three, then we need to return the sum of the two lower Fibbonacci numbers.
This is a horrible way of creating the Fibonacci sequence because it involves an exponentially large amount of function calls. But it works. And the reason it works is because the Fibbo in here, the variables inside it, are also disconnected from the Fibbo here and the Fibbo here. All these functions are called one inside the other, but they don't overwrite the variables.
So the v inside the inner Fibbo is different from the v inside the outer Fibbo and so on. So let me save this. OK, so this works. Now notice that if I try it with 25, it takes a bit of time. And 35 is almost too long to run. I'm not going to even wait for this to run.
This is calling 2 to the power 35 function calls, which is a little bit too many for me. And I'm going to cancel it-- ctrl c, cancel. And you can see here-- let me show you the trace-- all the function calls when it was stopped. It was stopped here.
But this was called from this line, and this was called from this line, and this was called from here. This is all the same line calling itself over and over again, each time lowering n by 1, until eventually n is 2. And then it can return the value.
It's that it keeps forgetting the value of the Fibonacci sequence when it needs it again. To fix that, let us keep a variable that will actually hold the Fibonacci sequence. So we initialize it with 1 1, which is the starting point. And now we will call a helper file-- helper function, that is. And we will return the value that is needed.
The helper function will guarantee that Fn is defined. Let's see how we do this. Here is the helper function. It doesn't have any return value, but it has an input. And all it does is checks if the number of elements in F is less than 10. And if it is, then it calculates the required one.
So first it calls helper with n minus 1, and then it says that Fn equals Fn minus 1, plus Fn minus 2. And then it's done. So the helper function guarantees that the Fibonacci sequence is updated up to n, this variable F, and then we just return the one we need.
So by this way, this assignment only happens once for every n, which makes it linear and end. Now we don't need all of this stuff. The only thing we do need is this final end.
Let me show you here. We want this function here. Sorry, we need another end. We want this function here to be embedded inside this function because what that does is it makes this variable F visible both for this function and for this function.
So this F and this F are the same variable. And the hover text says so-- the scope of variable F spans multiple functions. So let's see how that works. I'll save it. We call Fibbo2 is 3 and the answer is correct. 4, 5, and 35-- no problem, 45-- no problem, 55-- no problem.
This is a simple example of what's called dynamic programming. And this is a way of reducing an exponential recursive implementation into a linear one. Now, you can have more than one input variable, and you can have more than one output. But I suggest that you investigate that on your own.