1.8 Multi-Step Methods

1.8.1 Adams-Bashforth Methods

Measurable Outcome 1.15, Measurable Outcome 1.17, Measurable Outcome 1.18, Measurable Outcome 1.19

Adams-Bashforth methods are explicit methods of the form,

\[v^{n+1} - v^{n} = {\Delta t}\sum _{i=1}^ s \beta _ i f^{n+1-i}.\] (1.136)

Thus, the basic time derivative approximation remains the same for all \(p\) (i.e. \(du/dt\) is approximated by \((v^{n+1} - v^ n)/Dt\)) and the higher-order accuracy is achieved by using more values of \(f\).

\(p\)

\(\beta _1\)

\(\beta _2\)

\(\beta _3\)

\(\beta _4\)

1

1

     

2

\(\frac{3}{2}\)

\(-\frac{1}{2}\)

   

3

\(\frac{23}{12}\)

\(-\frac{16}{12}\)

\(\frac{5}{12}\)

 

4

\(\frac{55}{24}\)

\(-\frac{59}{24}\)

\(\frac{37}{24}\)

\(-\frac{9}{24}\)

Table 2: Coefficients for Adams-Bashforth methods (these methods are explicit so \(\beta _0 = 0\)). Note: the \(p=1\) method is the forward Euler method.

The coefficients for the first through fourth order methods are given in the table above. The first-order Adams-Bashforth is forward Euler.

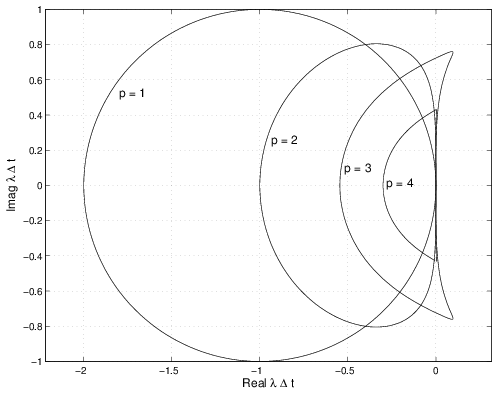
The graph shows the shrinking, but all overlapping, Adams-Bashforth stability regions for p=1 through p=4 methods.
Figure 1.19: Adams-Bashforth stability regions for \(p=1\) through \(p=4\) methods. Note: interior of contours is stable region.

The stability boundary for these methods are shown in Figure 1.19. As the order of accuracy increases, the stability regions become smaller. Note, this is the opposite of Runge-Kutta methods for which the size of the stability regions increases with increased accuracy (see Section 1.9).